信号与系统速通: 现代视角下的信号与系统理论体系

序言

本文创建于杭电 2025-2026-1 学期网安的信号与系统期末考试复习时. 全文可能比较长, 实际上是本人三个完整的地球日消化总结的结果.

文章不会覆盖信号与系统的内容, 仅仅可以被看作导论, 或是叫速通, 因此只会大致描述信号与系统的理论体系怎样用直观而不跳跃的思路得来. 为什么只有这些内容, 因为我是因为期末复习才开始学习信号与系统的.

什么是跳跃的思路? 实际上教材的思路就是跳跃的思路. 我们学习和发展一个学科的过程是这样的: 我们先用自然语言描述出一些公理, 而我们所有的理论成果都是由公理之间相组合得到的.

有意思一点的说法是, 如果把这个学科所有可能得到的理论成果视作一个向量空间, 那么公理就是这个向量空间的基向量, 显然我们的向量空间是由我们的基向量张成的. 你如果凭空提出一条公式, 你就不是在研究学科, 而是在创立新的学科. 但这却是目前我们的教材正在做的事情, 是和学习过程相悖的, 跟着这样的教材学出来思路也会是跳跃的思路. 我希望避免这一点.

本文决定从这样的角度出发, 重新审视信号与系统这门学科应当怎样被重新发现, 并且引出泛函分析可能的历史动机.

本人也是学生, 希望大家可以一起讨论, 广泛吸取大家的意见.

截至 2026.1.16, 本文尚未完成, 仅完成至怎样消除时变章节.

目录

什么是信号与系统

耳机功放, 大语言模型, 人类

TODO: 我需要一个更加有趣的一些现实例子, 引出为什么我们想抽象出系统这个词. 也许应该举出一些在信号与系统学科出现之前就出现的东西, 比如大桥. 风吹过大桥, 产生了振荡.

对信号和系统的抽象: 从“实体”到“关系”

我们创造了信号与系统这个概念. 我们用 $H$ 指代系统. 对系统输入 $x(t)$ 信号(激励), 系统对 $x(t)$ 做一系列复杂而无法直接测量的操作, 最终可以得到 $y(t)$ 信号(响应).

$$ \underset{\text{激励}}{x(t)} \rightarrow \underset{存在即被观察}{\boxed{H}} \rightarrow \underset{\text{响应}}{y(t)} $$

系统是复杂的, 我们不能直接测量一个系统, 系统之所以能存在, 取决于系统能被观察, 而观察的途径是测量它的输入和输出. 这话是不是颇有哲学意味? 我们不知道现实的放大器发生了什么, 却知道它放大了电压幅值. 我们很难直接知道一个现代大模型内部发生什么运算, 我们只能输入一段 token, 得到一段 token. 只能通过感知它的输入和输出. 我不知道你的大脑里想什么, 却只能知道我给你一段音频, 你返回一些音频.

如果用数学来表达信号, 很显然我们可以用函数. 但系统呢? 我们用什么数学工具描述一个系统?

描述系统的工具: 微分方程

如果你是学习过信号与系统的学生, 你当然知道我们一直在研究微分方程. 但是你是否思考过为什么信号与系统一定要研究那么多微分方程?

如果搞不清这个问题, 那不搞研究就变成做题了. 如果找不到做一件事情的意义, 我连一点做这件事的动力都没有.

信号与系统需要微分方程, 这一点并不是偶然想到的, 而是必然只能用微分方程. 现在我们来找我们刚刚想要的意义.

为什么一定是微分方程

微分方程有两个特点, 一个特点是微分, 另一个特点是方程. 这听起来像一句废话. 但这两个特点恰好完美符合我们的需求.

为什么是微分

既然我们只能通过输入和输出之间的变化来定义系统，那么我们需要一种能描述变化之间相关性的语言. 这涉及到一个哲学前提：

因果的连续性.

如果我们假设自然界的变化是连续的，那么系统在“这一秒”的状态，必然取决于它“前一毫秒”的状态, 以及当下的输入.

系统的特征不体现在某个孤立的时刻，而体现在状态改变的速率上.

输入（推力）会导致输出的改变（加速度/速度变化）。在数学上，改变的快慢就是导数（微分）!

因此我们想描述“输入”与“输出的变化”之间关系，我们自然而然只能用微分.

为什么是方程

我们如果进一步思考: 系统之所以被称为系统，是因为它遵循某种内在的法则. 比如能量是守恒的, 电荷是守恒的.

换句话说: 系统的物理属性（质量、电阻、弹性）实际上是输入和输出之间的比例约束。

我们要研究系统，其实是在找那个不变的规则。

这个规则通常表现为：输出的某种组合（比如位移和速度）必须平衡掉输入的能量。

微分方程本质上就是记录这种能量/信息流动。它告诉我们，为了维持某种物理平衡，输出及其各阶变化率必须与输入达成怎样的比例。

我们无法直接看到系统的“灵魂”，但可以看到它的“行为”。系统的行为不是静态的照片，而是一连串的反应过程。

既然是反应过程，就意味着输出的变化（导数）与当下的输入（函数值）之间存在某种固定的规则。微分方程正是捕捉这种‘瞬间’的相机, 把原本难以捉摸的内部构造，转化成了输入与输出之间必须遵守的规则.

总之我们现在发现了微分方程的特性符合我们的需求, 微分方程可以方便的表示输入的形式和输出的形式和关系, 却很难直接解出系统. 我们想分析系统, 其实就是想分析微分方程.

系统的线性和时变

看到标题懵了, 什么是时变什么是线性, 线性这个词竟然能描述一个系统? 慢慢解释一下, 我仅仅只是为了保证文章看起来有结构一点才把这个词摆到标题来.

我们刚刚提到了耳机功放的例子, 功放的学术一点的名字叫放大器.

我们理想上的放大器, 仅仅只把 $x(t)$ 电压信号的纵轴进行缩放, 对电压进行等比例放大或缩小, 对吧? $H$ 对 $x(t)$ 的作用是 $y(t)=Ax(t)$, 我们能类比为等比例函数, 显然它就是线性的.

但现实中的放大器是什么呢? 首先它有最大输出电压 $V_{dd}$, 那现在它就是分段函数. 显然这个时候不线性了, 它是分段的. 而且可能放大器对不同的信号放大效果也许不同, 中间的那条线甚至可能不是条直线而是扭扭曲曲的了. 超过了 $V_{dd}$, 功放就会爆音. 不完美输出 $x(t)$ 的等比例缩放, 这是功放的失真.

这意味着输出 $y(t)$ 是关于输入 $x(t)$ 的一个复杂函数 $f(x)$, 这就是系统的非线性.

Hifi 圈买来耳机想放一段时间音乐, 煲机, 才能达到更好播放效果. 功放随着电路发热、元件老化，可能耳机和功放的性能会下降. 显卡跑 3A 大作, 用着用着发热了, 性能下降, 帧数变低.

系统的参数 $A$ 会随时间 $t$ 漂移。这时系统变成了 $y(t)=A(t)⋅x(t)$. 这就是系统的时变.

如果我们直接研究这种现实中的系统，数学上会立刻陷入非线性时变微分方程的泥潭，这类方程大多没有通解，且对初始条件极度敏感. 因此我们想简化问题, 先看看简单的情况, 我们现在只研究线性时不变系统, 即: 线性的, 不随时间变化的系统, 翻译一下叫 Linear Time-Invariant System, 以后我们简称这样的系统叫 LTI 系统.

问题的简化: 消除非线性和时变

我们想简化问题, 只研究 LTI 系统, 换句话说我们不想有非线性和时变. 怎么在数学上表达我们的需求呢?

怎样消除非线性

如果我们把系统的响应函数 $f(x)$ 进行泰勒展开:

$$ f(x) = f(0) + f’(0)x + \frac{f’’(0)}{2!} x^2 + \frac{f’’’(0)}{3!} x^3 + \dots $$

你可以非常直观地看到, $f(x)$ 非线性的来源, 就是这些非线性项. 我们直接把非线性项人为置零, 并且消除偏置(去掉 $f(0)$, 假设没有输入就没有输出), 这就是数学上的线性.

$$ f(x) \approx Ax \quad (\text{其中 } A = f’(0), \text{ 忽略高阶项 } x^n) $$

结果我们就得到了 $y=Ax$ ,这就是线性化. 我们只抓住主要矛盾, 不看次要矛盾.

但这只是描述了怎样的函数才是线性的. 为什么微分方程也能是线性的呢? 这也是关键的一步跳跃。我们刚才说到, 我们要研究的不仅是 $y$ 和 $x$ 的关系，还有它们变化率的关系.

事实上我们可以发现, 微分运算本身也是线性的!

为什么这么说?

如果我们定义微分算子 $D$:

TODO: 此处直接提出算子是否不太合适?

$$ \hat{D} = \frac{d}{dt} $$

你会发现:

$$ \hat{D}[a \cdot x_1(t) + b \cdot x_2(t)] = a \frac{d x_1(t)}{dt} + b \frac{d x_2(t)}{dt} = a \hat{D}x_1(t) + b \hat{D}x_2(t) $$

此时我们的逻辑才完成了闭环: 既然我们通过泰勒展开把“函数关系”变线性了, 而且“微分运算”天生就是线性的, 那么把它们组合起来的微分方程 (例如 $a_n D^n y + … = b_m D^m y$ ) 也就自然可以继承这种线性特质.

怎样消除时变

我们刚才提到的“让输出与之前的输入不相干”, 在时间上体现为: 系统的记忆特质必须是恒定的。

时不变, 意味着系统对信号的“加工能力”不随时间流逝而改变。如果你今天给它一个信号，它这样反应；明天给它同样的信号，它还是一样的反应。

在微分方程中，这意味着描述系统特性的系数（如电阻 $R$、电感 $L$、质量 $m$）不能是时间 $t$ 的函数。

如果系数是常数，这就是常系数微分方程

如果系数随时间变 (如 $t^2 y′′ + t^2 y′ + y = x$), 自然, 系统就是时变的了.

我们现在费尽心思消除了非线性和时变, 不是为了偷懒, 这是从哲学上的思考出发的, 这是叠加原理.

  1. 因为系统是线性的，我们可以把复杂的信号拆解成无数个简单的“小信号”之和。
  2. 因为系统是时不变的，我们处理这些“小信号”时，不需要考虑它们发生的先后顺序。
  3. 最终目我们可以通过研究系统对一个最简单的信号的反应, 把这些最简单的反应进行叠加组合, 就能推导出它对任何复杂信号的反应。

因此我们的现在只会研究类似这样的方程:

$$ P(D)y(t) = Q(D)x(t), \quad D = \frac{d}{dt} \newline \text{其中,} \quad P(D) = \sum_{k=0}^{N} a_k D^k $$

零输入 LTI 系统: 齐次常微分方程

如果进一步简化问题, 只讨论零输入系统, 这意味着不再对 $x(t)$ 作考虑. 那么, 微分方程可能类似这样:

$$ A \frac{d^2 y(t)}{dt^2} + B \frac{d y(t)}{dt} + C y(t) = 0 $$

我们已经知道, 微分方程让我们能表示系统, 现在这个方程翻译一下就是, 这个系统跟输入没关系, 但和它自身的状态有关系. 这么说可能很抽象, 我们举一个现实中的例子你就会理解: 弹簧-质量-阻尼系统.

想象这样一个装置:

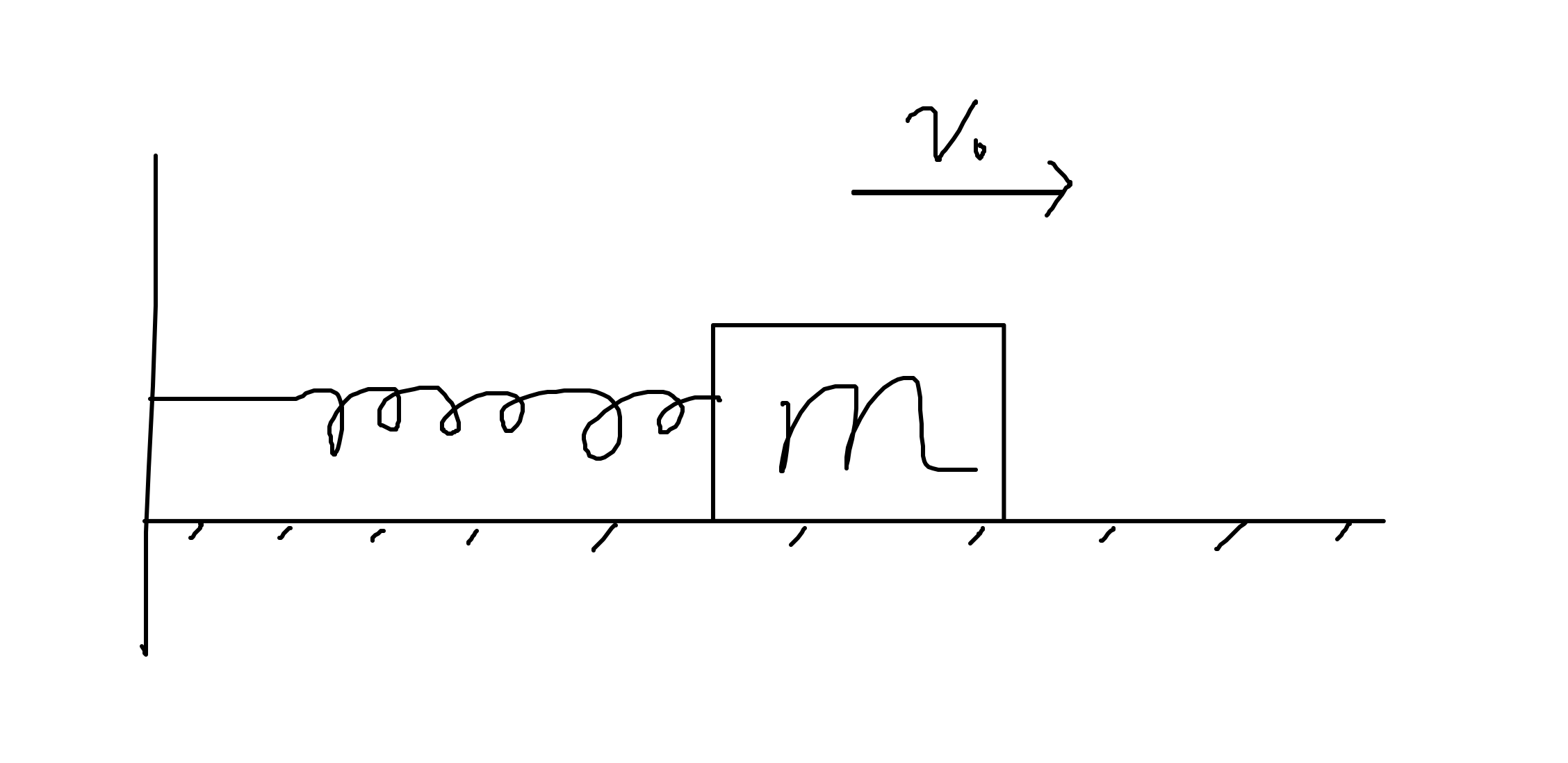
弹簧-质量-阻尼系统

一个质量块 $m$, 你知道 $F=ma$, 质量越大惯性越大越不爱动.

有阻尼系数 $c$ ,比如空气阻力, 阻尼可能随速度成正比 $c$.

有弹簧, 弹性系数 $k$, 拉的距离越大, 它往原点的力越大.

$$ my’’ + cy’ + ky = 0 $$

你把它拉开放手, 它就想弹回去, 有质量, 加速度低, 就刹不住车, 弹来弹去. 有阻尼, 振幅就越来越小, 最终就会归为原点.

我们此时现在实际上想研究的问题是, 我们好奇系统如果有这样的质量, 阻尼, 弹性系数时, 我们的弹簧会呈现怎样的运动.

换句话说, 我们想知道对于这样的方程, 如何找到 $y(t)$.

事实上你可以想到, 滑块根据它的初速度, 初始位置的不同, 肯定会有无穷多种运动样式, 有的振幅大有的振幅小, 有的先向左有的先向右.

我们想找到一个通解的模式, 这样就能根据系统的初始状态, 得到通解中的某一个特解.

问题来了, 我们的通解, 我们各种各样的 $y(t)$, 应该会长成什么样子呢?

我们这里虽然只是一个二阶的微分方程, 但别忘了我们实际上系统可能远比这个系统复杂, 可能 $y(t)$ 会被微分无数次. $y(t)$ 如果每微分一次, 就大变模样, 显然会难以适用于各种微分方程.

我们希望 $y(t)$ 最好可以只由一个初等函数组成, 并且这个初等函数对微分运算保持线性. 换句话说, 我们希望它反复求导的时候, 不会变的越来越复杂.

这样一来, 意味着我们在对它做微分运算时, 可以让我们抛掉 $t$ 的相关性, 对它微分不会产生新的关于 $t$ 的奇怪东西. 也就是每求一次导，只是多了一个常数, 再求一次导，也只是再多一个常数, 那它代进微分方程时，所有项就都能合并起来。

这样一来，微分方程中所有关于变化率的项，都可以被统一成同一个函数因子的倍数，问题就从“解函数”变成了“解常数”。

初等函数只有那么几个. 不管通过直觉, 还是通过排除法, 我们都能发现, 我们想要的函数实际上就是指数函数:

$$ \frac{de^{\blacksquare t}}{dt} = \blacksquare e^{\blacksquare t} $$

我们如果就真的让 $y(t) = e^{\blacksquare t}$, 此时:

$$ A\blacksquare^2 e^{\blacksquare t} + B\blacksquare e^{\blacksquare t} + Ce^{\blacksquare t} = 0 $$

这时候, 正如我们刚刚所料, 发现 $e^t$ 果然可以提取, 就是:

$$ e^{\blacksquare t}(A\blacksquare^2 + B\blacksquare + C) = 0 $$

指数函数, 这样一个初等函数, 确实可以让我们在不用关心 $t$ 的情况下就可以表示出这个系统.

方框的 latex \blacksquare 打的有点累, 所以我后面就把它写成 $s$. 你知道它就只是个符号而已. 你是信号与系统的发明者, 你可以自己发明任何符号.

$$ e^{st}(As^2 + Bs + C) = 0 $$

总之, 我们想分析零输入的线性时不变系统, 想分析那种刚刚复杂的 n 阶常微分方程, 竟然可以在不丢失任何信息的情况下, 只需要分析一个简单的多项式:

$$ As^2 + Bs + C = 0 $$

要让上面的微分方程成立, 只需要让这个多项式成立.

它其实被叫做特征方程, 名字很好理解, 它就是这个系统的特征.

刚刚说到因为这是一个线性系统, 实际上微分方程的解我们可以想象到是 $e^{st}$ 在 s 取不同值时候的线性组合. 我们想象微分方程的解空间是一个矩阵空间, 那 $e^{st}$ 实际上是这个空间的基变量, 通解实际上是基变量张成的空间.

我们选择 $e^{st}$ 作为“基函数”, 本质上是因为它是微分运算的"本征函数", 这里暂时不展开说.

因为这里讨论的是二阶, 所以通解应该可以写成

$$ y(t) = ae^{s_1 t} + be^{s_2 t} $$

我们其实还没把方程解完. 最终我们想让 $s$ 里只包含 ABC. 简单想到用一元二次的求根公式:

$$ s_1 = \frac{-B+\sqrt{B^2-4AC}}{2A} \newline s_2 = \frac{-B-\sqrt{B^2-4AC}}{2A} $$

但这样明显是有问题的, 不能直接把 $s_1$, $s_2$ 带入进去. 我们会发现其实需要分情况讨论这个 $s$.

$$ \Delta = 0, s_1 = s_2 = \frac{-B}{2A}, 重根 \newline \Delta > 0, s_1, s_2 \in \mathbb{R} $$

当 $\Delta < 0$ 时, 我们已经需要讨论 $s$ 是一个复数的情况, 我们一般把 $s$ 表示成 $\alpha + j\omega$. 利用欧拉公式可以把 $e^{st}$ 做这样的变换:

$$ e^{st} = e^{(\alpha + j\omega)t} = e^{\alpha t} e^{j\omega t} \newline e^{st} = e^{\alpha t}(\cos{\omega t} + j\sin{\omega t}) $$

上面的求根公式的实部和虚部可以由此对应到这样的实部和虚部:

$$ \alpha = -\frac{B}{2A} \quad,\quad \omega = \frac{\sqrt{4AC - B^2}}{2A} $$

至此我们求完了这样一个微分方程, 的通解. 注意感受一下, 微分方程的解是函数. 理解一下特解, 特解是什么? 比如给定: $y(0)$ 和 $y’(0)$, 我们当然可以找到这样的系统状态对应的输出 $y(t)$ 的确切函数形式, 这个函数形式当然是符合通解的格式的. 或者说, 这个特解函数就是通解空间中的一个具体的向量.

思考:

  1. 为什么我们只要两个不同的 $e^{st}$ 就可以表示出通解? 为什么不是三个?
  2. 为什么

有输入的 LTI 系统

现在进一步思考, 现在看有输入的 LTI 系统. 换成微分方程的语言, 形式可能长这样(注意为了直观感受, 仍然只看二阶常微分方程, 实际上系统可以是 n 阶):

$$ A \frac{d^2 y(t)}{dt^2} + B \frac{d y(t)}{dt} + C y(t) = D \frac{d^2 x(t)}{dt^2} + E \frac{d x(t)}{dt} + F x{t} $$

我们已经知道怎么处理这样的问题了, 我们可以只研究特征方程.

狄拉克函数

有没有有种函数信号, 适用于所有的系统, 作为统一度量衡, 激发出的函数可以显露系统所有模态?

想适用于所有系统, 意味着时间无关, 并且能量有限, 自然能想到如何构造.

卷积的本质是函数分解

思考能否把系统对信号的作用写成函数形式.

$\delta (t)$ 得到 $h(t)$.

$x(t)$ 得到 $y(t)$

$x(t)$ 本质可以分解为无数个 $\delta(t)$ 时移后的加权和, 时移的长度就是 $t_0$, 权就是 $x(t)$. 因此 $x(t)$ 应该可以被写成积分:

$$ x(t) = \int_{-\infty}^{\infty} x(t)\delta(t-\tau) d\tau $$

我们知道一个 $\delta(t)$ 会激发出对应时移加权之后的 $h(t)$, $y(t)$ 应当也可以写成无数个 $h(t)$ 的时移加权和.

$$ y(t) = \int_{-\infty}^{\infty} y(t)h(t-\tau) d\tau $$

但 $y(t)$ 应该也可以分解到 $\delta(t)$ 上.

我们现在可以发明卷积. 我们用函数的方式表示出时域上表示系统对信号的作用, 这个作用是 $h(t)$

$$ x(t)*h(t) = \int_{-\infty}^{\infty} x(\tau) h(t - \tau) d\tau $$

初步思考拉普拉斯变换

这个计算是复杂的. 但我们刚刚发现特征方程之间的计算是简单的. 并且我们似乎找到了一个方式能从 $x(t)$ 获得 $X(s)$. 我们有这两个方程:

$$ x(t) * h(t) = y(t) \newline X(s)H(s) = Y(s) $$

假如我们能找到一种运算, 定义出它, 以及它的逆运算, 那么我们在计算 $x(t)*h(t)$ 的时候, 就可以做到直接用这个运算, 把 $x(t)$ 和 $h(t)$ 变成 $X(s)$ 和 $H(s)$, 我们就只需要计算 $X(s)H(s)=Y(s)$ 这样的单次乘法运算, 再把 $Y(s)$ 逆运算回 $y(t)$ 就可以得到结果.

那么我们怎样找到这个运算呢?

希尔伯特空间

如果把函数看作无限维向量, $x(t)$ 和 $X(s)$ 各自构成了自己的函数空间. 想找到拉普拉斯变换, 实际上想找到两个函数空间之间的映射关系.

我们需要先想办法定义函数空间. 空间需要有正交基. 向量和向量之间的正交是靠内积定义的, 内积为 0 则正交. 那么需要先定义函数的内积是什么.

内积运算, 是两个向量之间的运算, 得到一个数值而不是向量. 意味着函数和函数的内积应该是值而不是另一个函数, 意味着需要积分.

注意我们的函数参数和值是复数域, 意味着复数域上的方向性也需要消除. 实现的办法是取虚数的共轭.

因此定义函数内积如下:

$$ <x(t), y(t)> = \int_{-\infty}^{\infty} x(t)y^*(t) dt $$

想找到两个函数空间之间的映射关系, 只要找到两个空间各自的正交基是什么.

对于 $x(t)$ 领域, 正交基实际上是 $\delta(t)$, 因为不同时间上的函数值完全没有干涉, 换句话说只在一个点取值.

对于 $X(s)$ 领域, 正交基我们现在实际上没有什么头绪. 可以通过微分方程的解的形式猜到可能是 $e^{st}$, 但这个思维是跳跃的.

如何考虑下一步要研究什么呢?

思考所有的线性常微分方程: 由 t 到 s

我们思考所有的线性常微分方程

$$ \sum_{i=1}^{n=\infty} C_i \frac{d^i y}{dt^i} = \sum_{i=1}^{n=\infty} D_i \frac{d^i x}{dt^i} $$

我们研究的对象是所有的线性常微分方程时, 我们讨论的自变量其实不再是 $y(t)$ 或者说 $t$

我们的自变量变成了微分方程的系数和阶数

而 $s$ 我们刚刚知道是关于系数和阶数的多项式, $s$ 由多项式定理可知会覆盖整个复平面.

$s$ 应当也可以作为一个自变量被讨论

思考:

  1. 为什么这里想到我们应该回去思考所有的线性常微分方程?
  2. 发现 $s$ 可以稠密覆盖整个复平面时, 为什么想到 $s$ 可以被作为自变量?

e^st 的振荡: 频率

观察 $s$ 在不同取值时的 $e^{st}$ 的特性, 发现有振荡和不振荡两种情况. 为什么会出现振荡?

$$ e^{\alpha + j\omega t} = e^{\alpha t}(\cos{\omega t} + j\sin{\omega t}) $$

用欧拉公式理解, 我们发现了振荡的原因是 $s$ 的虚部, 而 $s$ 的实部控制了 $e^{st}$ 的幅值变化.

由此我们才能定义出频率是什么.

傅里叶分析

我们好奇的是 $e^{st}$ 的振荡特征. 因此我们现在只看导致它产生振荡的虚部, 即: $e^{j\omega t}$

傅里叶级数

我们发现:

  1. 三角函数似乎是世界的一种基本量
  2. 不同频率的正弦波似乎不会相互干扰
  3. 就像把写成泰勒展开一样, 似乎周期信号可以写成多个正弦波的叠加

由 2, 不相干 -> 正交 -> 点积为 0

我们给不同的正弦波定义点积:

$$ f_1 \cdot f_2 = \int_{0}^{T} f_1(t)f_2(t) dt $$

这里和上面想到的函数内积不太一样, 我们没有复数, 只是周期函数, 没必要讨论共轭.

$$ f_1(t) = \cos{n \omega_0 t}, \quad f_2(t) = \cos{m \omega_0 t} \newline \int_{0}^{T} \cos{n \omega_0 t} \cos{m \omega_0 t} \ dt = \int_{0}^{T} \frac{1}{2} (\cos{(n+m) \omega_0 t} + \cos{(n-m) \omega_0 t}) \ dt $$

公式:

$$ f(t) = \sum_{n=-\infty}^{+\infty} D(m) e^{j m \omega_0 t}\newline D(m) = \frac{1}{T} \int_{0}^{T} f(t) e^{-j m \omega_0 t} $$

傅里叶变换

考虑非周期信号, 实际上非周期信号可以被看作是周期为无穷的周期信号.

$$ X(j\omega) = \int_{-\infty}^{\infty}x(t)e^{-j\omega t} \ dt \newline x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(j\omega) e^{j\omega t} \ dt $$

对偶性

如果 时域的 f(t) 对应到频域的 F(w), 那么时域的 F(t) 对应到 f(w),

拉普拉斯变换: 带上实部

傅里叶变换在积分之后形式显得丑陋, 其实暗示了它是不完备的. 我们知道为什么不完备, 我们没有考虑实部.

带上实部之后就有了拉普拉斯变换.

$$ F(s) = \mathcal{L} { f(t) } = \int_{0}^{\infty} f(t) e^{-st} \ dt $$

$$ f(t) = \mathcal{L}^{-1}{F(s)} = \frac{1}{2\pi j} \int_{\gamma -j\infty}^{\gamma + j\infty} F(s)e^{st} \ ds $$

再次思考微分方程: 微分方程的完全解

引入算子视角

我们已经定义了 LTI 系统。

问题： 用微分方程 $y′′(t)+ay′(t)+by(t)=x(t)$ 描述系统太笨重了。

微分方程和差分方程如果不把 $D$（微分/差分）看作运算，而看作一个对象（算子），那么系统 $H$ 就是基础算子 $D$ 的有理函数 Rational Function

抽象： 引入微分算子 $D$ ,方程变成 $(D^+aD+b)y=x$。

定义系统算子： $H=\frac{1}{D^2+aD+b}$ 即，系统是基础算子 D 的有理函数

算子代数, 系统的本质

我们能不能像操作代数式一样操作 $D$ 和 $H$?

  1. 算子的代数结构 (交换律,结合律)：
    1. 为了像操作数一样操作系统（串联、并联），必须定义算子的加法和乘法。
    2. 必须证明算子满足交换律（$H\cdot D=D\cdot H$）和结合律($D\cdot D = D^2$)。
    3. 证明: 只有在 LTI 下，算子才满足交换律。正因为系统是 时不变 (TI) 的，系统算子 H 才能和延时/微分算子 D 交换.

特征函数和谱

回到初衷, 解微分方程太难，我们想把“卷积/微分”变成“乘法”

  1. 因为算子满足交换律（特别是与微分/移位算子可交换），根据线性代数, 可交换矩阵拥有共同的特征向量，系统算子 $H$ 必然共享基础算子 $D$ 的特征函数。
  2. $D$（微分）的特征函数是 $e^{st}$ ；$D$（差分）的特征函数是 $z^n$ (想到等比数列)。
  3. 特征值
  4. 因此，$e^{st}$ 和 $z^n$ 也就成了整个 LTI 系统分别在连续和离散领域的特征函数。这是拉普拉斯变换和 Z 变换存在的根本原因。

什么是算子谱

  1. 线性代数的类比

    1. 矩阵是有限维空间上的线性算子。
    2. 矩阵的特征值构成的集合，叫"谱"。有且只有无限连续才能叫谱, 这里不应该叫谱
    3. 如果 $Av=λv$，输入向量 v 经过矩阵变换后，方向不变，只伸缩了 $λ$ 倍。

  2. 推广到函数空间(泛函分析)

    1. 系统 $H$ 是无穷维函数空间上的线性算子。
    2. 信号 $f(t)$ 是这个空间里的向量。
    3. 我们需要寻找一种信号，通过系统后，波形（“方向”）不变，只有幅度/相位（“长度”）发生了变化。即：$H{f(t)}=λ⋅f(t)$。
    4. 这种信号就是特征函数（$e^{st}$）。
    5. 对应的 $λ$（也就是系统对该频率信号的增益），构成了系统的谱。

  3. 结论 系统的“频率响应”或者“传递函数” 即 $H(s)$ 或 $H(jω)$，本质上就是系统算子的“谱”。

LTI 的情况下, 谱定理保证了：任何 LTI 系统都可以分解为一系列特征函数（正弦波/指数波）的加权叠加。处理信号变成了处理这些特征值（谱）。

分析离散（从函数到数列）

  1. 离散化的动机： 计算机只能处理离散信号（数组）
  2. 采样的本质
    1. 时域：连续信号 x(t) 乘以周期冲击串
    2. 频域: 时域相乘等于频域卷积。连续信号的频谱与冲击串的频谱（也是冲击串）卷积 → 导致原频谱的周期延拓
      1. 混叠(延拓部分发生重叠)
  3. 频率的定义从模拟到数字频率 $\omega = \Omega T$

幺正算子

如果 $<x(t), y(t)> = <T{x(t)}, T{y(t)}> $ 那么 $T T^* = I$ 且 $T^* = T^{-1}$

令 $x(t) = y(t)$, $<x(t), x(t)> = |x(t)|^2$, 定义算子内积:

$$